3.1. Menerapkan Logika dan Algoritma Komputer

I. Logika 

Logika  berasal dari dari bahasa Yunani yaitu  LOGOS  yang berarti “ ilmu” . Logika dapat diartikan ilmu yang mengajarkan cara berpikir untuk  Melakukan aksi dengan tujuan tertentu.

A. Operasi Logika

 Operasi dapat membentuk pernyataan majemuk :

1. Negasi / Lingkaran ( kata perangkai : tidakhlah benar ) simbol  "～"
2. Konjungsi ( kata perangkai : dan ) simbol  "⋀"
3. Disjungsi ( kata perangkai : atau ) simbol  "⋁"
4. Implikasi ( kata perangkai : jika ) simbol  "=>"
5. Biimplikasi ( kata perangkai : ....jika & hanya jika.... ) simbol  "<=>" 

Contoh :

1. Ani dan Ana anak kembar  ( konjungsi )
2. Jika  X = 0  maka  X² = X   ( implikasi )
3. Suatu segitiga dikatakan segitiga sama sisi jika dan hanya jika ketiga sudutnya sama  ( biimplikasi )

B. Pernyataan Tunggal dan Majemuk

• Pernyataan Tunggal (sederhana) adalah Pernyataan yang tidak memuat pernyataan lain/sebagai-bagiannya.

Contoh : Jakarta adalah Ibu Kota Indonesia 

• Pernyataan Majemuk adalah kalimat bantu yang diperoleh dengan cara menggabungkan beberapa pernyataan tungal.

Contoh : Jika suatu bilangan habis dibagi 2 maka bilangan itu bulat

C. Tabel Kebenaran 

1. Operasi Negasi/ingkaran : Jika p suatu pernyataan benilai benar, maka  ~p bernilai salah dan sebaliknya jika p bernilai salah maka ~p bernilai benar.
   
2. Operasi Konjungsi : Jika komponen p dan q suatu pernyataan bernilai benar, maka p⋀q akan bernilai benar, dan jika salah satu komponennya bernilai salah maka akan bernilai salah.
   
3. Operasi Disjungsi : Sebuah Disjungsi akan bernilai salah jika komponen p dan q bernilai salah, dan akan bernilai benar jika salah satu dari komponennya bernilai benar.
   
4. Operasi Implikasi : Sebuah pernyataan bernilai salah jika antesedennya ( awal ) benar & konsekwennya ( akhir ) salah, dalam kemungkinan lainnya implikasi akan bernilai benar.
   
5. Operasi Biimplikasi : Sebuah pernyataan bernilai salah jika nilai p dan q tidak sama, jika nilai p dan q sama maka pernyataan tersebut akan bernilai benar.
   
   Contoh :
   (~p ∧ r) ∨ (~r ⇒ q)

 Bentuk - Bentuk Pernyataan :

1. Kontradiksi : Suatu bentuk pernyataan yang hanya mempunyai contoh substitusi yang salah, atau sebuah pernyataan majemuk yang salah dalam segala hal tanpa memandang nilai kebenaran dari komponen-komponennya.

2. Tautologi :  Sebuah pernyataan majemuk yang benar dalam segala hal, tanpa memandang nilai kebenaran dari komponen-komponennya.

3. Kontingensi : Sebuah pernyataan yang bukan suatu tautologi maupun kontradiksi.

II. Algoritma

Algoritma  dapat diartikan urutan langkah-langkah  (instruksi-instruksi / aksi-aksi)  terbatas untuk menyelesaikan suatu 

masalah. 

Dari pengertian diatas maka dapat diartikan  Logika dan  Algoritma  adalah ilmu yang mempelajari cara penyelesaian masalah berdasarkan langkah-langkah terbatas yang logis dan sistematis dengan tujuan tertentu.

Contoh Algoritma:

Permasalahan:

Diberikan dua  gelas  (A dan B),  gelas  A berisi air kopi dan  gelas  B berisi air teh. Pertukarkan isi  gelas  tersebut sehingga menghasilkan  gelas  A semula berisi air kopi menjadi berisi air teh dan  gelas  B yang semula berisi air teh menjadi berisi air kopi.

Penyelesaian:

Untuk mempertukarkan isi  gelas  dengan benar, maka diperlukan  gelas tambahan yang kita namakan  gelas  C  sebagai tempat penampungan sementara.  Berikut Algoritmanya:

Kasus :

Tukarkan nilai 2 variable (A dan B) yang nilainya di-input-kan!

Latihan:

Algortima Tukar_Isi_Gelas Ada dua gelas (gelas A dan gelas B), gelas A berisi Kopi dan gelas B berisi Teh. Pertukarkan isi kedua gelas tersebut sehingga gelas A yang  semula berisi Kopi menjadi berisi Teh dan gelas B yang semula berisi Teh menjadi berisi Kopi.

Deskripsi

1. Tuangkan isi gelas A ke gelas C

2. Tungkan isi gelas B ke gelas A

3. Tuangkan isi gelas C ke gelas B

Hasil akhir dari algoritma pertukaran isi gelas menjadi:

A : berisi Teh

B : berisi air Kopi

Syarat-Syarat Algoritma 

Syarat-Syarat Algoritma menurtu Donald E. Knuth, yaitu:

1.  Finiteness (Keterbatasan)

Algoritma harus berakhir setelah melakukan sejumlah langkah proses

2.  Definiteness (Kepastian)

Setiap langkah algoritma harus didefinisikan dengan tepat dan tidak menimbulkan makna ganda

3.  Input  (Masukan)

Sebuah algoritma memiliki nol atau lebih masukan (input) yang diberikan kepada algoritma sebelum dijalankan

4.  Output (Keluaran)

Setiap algoritma memberikan satu atau beberapa hasil keluaran

5.  Effectiveness  (Efektivitas)

Langkah-langkah algoritma dikerjakan dalam waktu yang “wajar”.

 III. Flowchart

A. Pengertian Dasar Flowchart

Definisi flowchart secara sederhana adalah:

- Penggambaran langkah-langkah atau urutan-urutan prosedur suatu aktivitas/program dalam bentuk grafik.

- Bagan-bagan sebagai simbol arus yang menggambarkan langkah-langkah penyelesaian suatu masalah/aktivitas/program.

Intinya flowchart adalah bagan untuk menggambarkan urutan langkah penyelesaian masalah.

B. Tujuan pembuatan flowchart

Setelah mengetahui definisi flowchart, maka kita akan dengan mudah mengetahui tujuan dibuatnya flowchart ini. 

Tujuannya adalah:

- Menolong para analis untuk memecahkan masalah ke dalam bagian-bagian yang lebih kecil untuk menyederhanakan masalah.

- Membantu para analis untuk menganalisis alternatif-alternatif pemecahan masalah.

- Mempermudah penyelesaian masalah termasuk dalam masalah dalam kehidupan sehari-hari.

- Menjadi alat untuk menggambarkan suatu tahapan penyelesaian masalah.

C. Simbol flowchart yang sederhana 

Simbol pada flowchart terbagi tiga jenis, yaitu:

1. Simbol alur/arus atau flow.

2. Simbol proses.

3. Simbol input/output.

Di bawah ini adalah simbol-simbol yang biasa dipakai dalam kehidupan sehari-hari.

 

Contoh :  
1.  Proses Memasak


2.

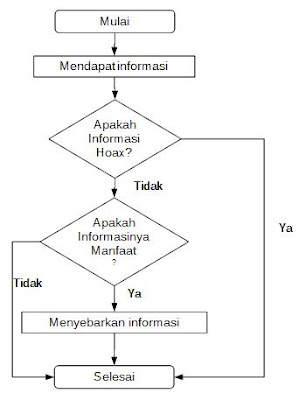
2. Proses untuk menentukan apakah menyebarkan informasi atau tidak